This post is the third in the series ECC: a gentle introduction.

In the previous posts, we have seen what an elliptic curve is and we have defined a group law in order to do some math with the points of elliptic curves. Then we have restricted elliptic curves to finite fields of integers modulo a prime. With this restriction, we have seen that the points of elliptic curves generate cyclic subgroups and we have introduced the terms base point, order and cofactor.

Finally, we have seen that scalar multiplication in finite fields is an “easy” problem, while the discrete logarithm problem seems to be “hard”. Now we’ll see how all of this applies to cryptography.

Domain parameters

Our elliptic curve algorithms will work in a cyclic subgroup of an elliptic curve over a finite field. Therefore, our algorithms will need the following parameters:

• The prime $p$ that specifies the size of the finite field.
• The coefficients $a$ and $b$ of the elliptic curve equation.
• The base point $G$ that generates our subgroup.
• The order $n$ of the subgroup.
• The cofactor $h$ of the subgroup.

In conclusion, the domain parameters for our algorithms are the sextuple $(p, a, b, G, n, h)$.

Random curves

When I said that the discrete logarithm problem was “hard”, I wasn’t entirely right. There are some classes of elliptic curves that are particularly weak and allow the use of special purpose algorithms to solve the discrete logarithm problem efficiently. For example, all the curves that have $p = hn$ (that is, the order of the finite field is equal to the order of the elliptic curve) are vulnerable to Smart’s attack, which can be used to solve discrete logarithms in polynomial time on a classical computer.

Now, suppose that I give you the domain parameters of a curve. There’s the possibility that I’ve discovered a new class of weak curves that nobody knows, and probably I have built a “fast” algorithm for computing discrete logarithms on the curve I gave you. How can I convince you of the contrary, i.e. that I’m not aware of any vulnerability? How can I assure you that the curve is “safe” (in the sense that it can’t be used for special purpose attacks by me)?

In an attempt to solve this kind of problem, sometimes we have an additional domain parameter: the seed $S$. This is a random number used to generate the coefficients $a$ and $b$, or the base point $G$, or both. These parameters are generated by computing the hash of the seed $S$. Hashes, as we know, are “easy” to compute, but “hard” to reverse.

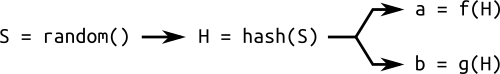
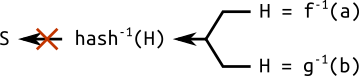
A curve generated through a seed is said to be verifiably random. The principle of using hashes to generate parameters is known as “nothing up my sleeve”, and is commonly used in cryptography.

This trick should give some sort of assurance that the curve has not been specially crafted to expose vulnerabilities known to the author. In fact, if I give you a curve together with a seed, it means I was not free to arbitrarily choose the parameters $a$ and $b$, and you should be relatively sure that the curve cannot be used for special purpose attacks by me. The reason why I say “relatively” will be explained in the next post.

A standardized algorithm for generating and checking random curves is described in ANSI X9.62 and is based on SHA-1. If you are curious, you can read the algorithms for generating verifiable random curves on a specification by SECG (look for “Verifiably Random Curves and Base Point Generators”).

I’ve created a tiny Python script that verifies all the random curves currently shipped with OpenSSL. I strongly recommend you to check it out!

Elliptic Curve Cryptography

It took us a long time, but finally here we are! Therefore, pure and simple:

1. The private key is a random integer $d$ chosen from $\{1, \dots, n - 1\}$ (where $n$ is the order of the subgroup).
2. The public key is the point $H = dG$ (where $G$ is the base point of the subgroup).

You see? If we know $d$ and $G$ (along with the other domain parameters), finding $H$ is “easy”. But if we know $H$ and $G$, finding the private key $d$ is “hard”, because it requires us to solve the discrete logarithm problem.

Now we are going to describe two public-key algorithms based on that: ECDH (Elliptic curve Diffie-Hellman), which is used for encryption, and ECDSA (Elliptic Curve Digital Signature Algorithm), used for digital signing.

Encryption with ECDH

ECDH is a variant of the Diffie-Hellman algorithm for elliptic curves. It is actually a key-agreement protocol, more than an encryption algorithm. This basically means that ECDH defines (to some extent) how keys should be generated and exchanged between parties. How to actually encrypt data using such keys is up to us.

The problem it solves is the following: two parties (the usual Alice and Bob) want to exchange information securely, so that a third party (the Man In the Middle) may intercept them, but may not decode them. This is one of the principles behind TLS, just to give you an example.

Here’s how it works:

1. First, Alice and Bob generate their own private and public keys. We have the private key $d_A$ and the public key $H_A = d_AG$ for Alice, and the keys $d_B$ and $H_B = d_BG$ for Bob. Note that both Alice and Bob are using the same domain parameters: the same base point $G$ on the same elliptic curve on the same finite field.

2. Alice and Bob exchange their public keys $H_A$ and $H_B$ over an insecure channel. The Man In the Middle would intercept $H_A$ and $H_B$, but won’t be able to find out neither $d_A$ nor $d_B$ without solving the discrete logarithm problem.

3. Alice calculates $S = d_A H_B$ (using her own private key and Bob’s public key), and Bob calculates $S = d_B H_A$ (using his own private key and Alice’s public key). Note that $S$ is the same for both Alice and Bob, in fact: $$S = d_A H_B = d_A (d_B G) = d_B (d_A G) = d_B H_A$$

The Man In the Middle, however, only knows $H_A$ and $H_B$ (together with the other domain parameters) and would not be able to find out the shared secret $S$. This is known as the Diffie-Hellman problem, which can be stated as follows:

Given three points $P$, $aP$ and $bP$, what is the result of $abP$?

Or, equivalently:

Given three integers $k$, $k^x$ and $k^y$, what is the result of $k^{xy}$?

(The latter form is used in the original Diffie-Hellman algorithm, based on modular arithmetic.)

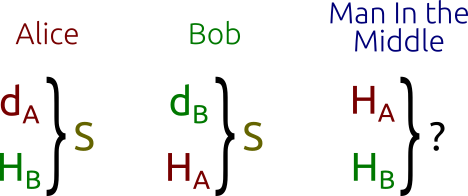
The principle behind the Diffie-Hellman problem is also explained in a great YouTube video by Khan Academy, which later explains the Diffie-Hellman algorithm applied to modular arithmetic (not to elliptic curves).

The Diffie-Hellman problem for elliptic curves is assumed to be a “hard” problem. It is believed to be as “hard” as the discrete logarithm problem, although no mathematical proofs are available. What we can tell for sure is that it can’t be “harder”, because solving the logarithm problem is a way of solving the Diffie-Hellman problem.

Now that Alice and Bob have obtained the shared secret, they can exchange data with symmetric encryption.

For example, they can use the $x$ coordinate of $S$ as the key to encrypt messages using secure ciphers like AES or 3DES. This is more or less what TLS does, the difference is that TLS concatenates the $x$ coordinate with other numbers relative to the connection and then computes a hash of the resulting byte string.

Playing with ECDH

I’ve created another Python script for computing public/private keys and shared secrets over an elliptic curve.

Unlike all the examples we have seen till now, this script makes use of a standardized curve, rather than a simple curve on a small field. The curve I’ve chosen is secp256k1, from SECG (the “Standards for Efficient Cryptography Group”, founded by Certicom). This same curve is also used by Bitcoin for digital signatures. Here are the domain parameters:

• $p$ = 0xffffffff ffffffff ffffffff ffffffff ffffffff ffffffff fffffffe fffffc2f
• $a$ = 0
• $b$ = 7
• $x_G$ = 0x79be667e f9dcbbac 55a06295 ce870b07 029bfcdb 2dce28d9 59f2815b 16f81798
• $y_G$ = 0x483ada77 26a3c465 5da4fbfc 0e1108a8 fd17b448 a6855419 9c47d08f fb10d4b8
• $n$ = 0xffffffff ffffffff ffffffff fffffffe baaedce6 af48a03b bfd25e8c d0364141
• $h$ = 1

(These numbers were taken from OpenSSL source code.)

Of course, you are free to modify the script to use other curves and domain parameters, just be sure to use prime fields and curves Weierstrass normal form, otherwise the script won’t work.

The script is really simple and includes some of the algorithms we have described so far: point addition, double and add, ECDH. I recommend you to read and run it. It will produce an output like this:

Curve: secp256k1
Alice's private key: 0xe32868331fa8ef0138de0de85478346aec5e3912b6029ae71691c384237a3eeb
Alice's public key: (0x86b1aa5120f079594348c67647679e7ac4c365b2c01330db782b0ba611c1d677, 0x5f4376a23eed633657a90f385ba21068ed7e29859a7fab09e953cc5b3e89beba)
Bob's private key: 0xcef147652aa90162e1fff9cf07f2605ea05529ca215a04350a98ecc24aa34342
Bob's public key: (0x4034127647bb7fdab7f1526c7d10be8b28174e2bba35b06ffd8a26fc2c20134a, 0x9e773199edc1ea792b150270ea3317689286c9fe239dd5b9c5cfd9e81b4b632)
Shared secret: (0x3e2ffbc3aa8a2836c1689e55cd169ba638b58a3a18803fcf7de153525b28c3cd, 0x43ca148c92af58ebdb525542488a4fe6397809200fe8c61b41a105449507083)

Ephemeral ECDH

Some of you may have heard of ECDHE instead of ECDH. The “E” in ECDHE stands for “Ephemeral” and refers to the fact that the keys exchanged are temporary, rather than static.

ECDHE is used, for example, in TLS, where both the client and the server generate their public-private key pair on the fly, when the connection is established. The keys are then signed with the TLS certificate (for authentication) and exchanged between the parties.

Signing with ECDSA

The scenario is the following: Alice wants to sign a message with her private key ($d_A$), and Bob wants to validate the signature using Alice’s public key ($H_A$). Nobody but Alice should be able to produce valid signatures. Everyone should be able to check signatures.

Again, Alice and Bob are using the same domain parameters. The algorithm we are going to see is ECDSA, a variant of the Digital Signature Algorithm applied to elliptic curves.

ECDSA works on the hash of the message, rather than on the message itself. The choice of the hash function is up to us, but it should be obvious that a cryptographically-secure hash function should be chosen. The hash of the message ought to be truncated so that the bit length of the hash is the same as the bit length of $n$ (the order of the subgroup). The truncated hash is an integer and will be denoted as $z$.

The algorithm performed by Alice to sign the message works as follows:

1. Take a random integer $k$ chosen from $\{1, \dots, n - 1\}$ (where $n$ is still the subgroup order).
2. Calculate the point $P = kG$ (where $G$ is the base point of the subgroup).
3. Calculate the number $r = x_P \bmod{n}$ (where $x_P$ is the $x$ coordinate of $P$).
4. If $r = 0$, then choose another $k$ and try again.
5. Calculate $s = k^{-1} (z + rd_A) \bmod{n}$ (where $d_A$ is Alice’s private key and $k^{-1}$ is the multiplicative inverse of $k$ modulo $n$).
6. If $s = 0$, then choose another $k$ and try again.

The pair $(r, s)$ is the signature.

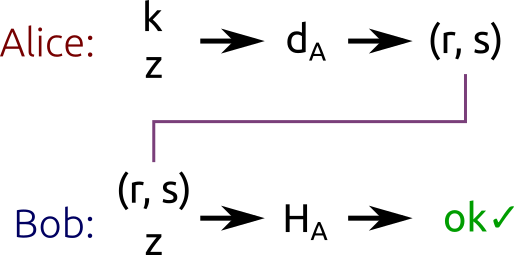
In plain words, this algorithm first generates a secret ($k$). This secret is hidden in $r$ thanks to point multiplication (that, as we know, is “easy” one way, and “hard” the other way round). $r$ is then bound to the message hash by the equation $s = k^{-1} (z + rd_A) \bmod{n}$.

Note that in order to calculate $s$, we have computed the inverse of $k$ modulo $n$. We have already said in the previous post that this is guaranteed to work only if $n$ is a prime number. If a subgroup has a non-prime order, ECDSA can’t be used. It’s not by chance that almost all standardized curves have a prime order, and those that have a non-prime order are unsuitable for ECDSA.

Verifying signatures

In order to verify the signature we’ll need Alice’s public key $H_A$, the (truncated) hash $z$ and, obviously, the signature $(r, s)$.

1. Calculate the integer $u_1 = s^{-1} z \bmod{n}$.
2. Calculate the integer $u_2 = s^{-1} r \bmod{n}$.
3. Calculate the point $P = u_1 G + u_2 H_A$.

The signature is valid only if $r = x_P \bmod{n}$.

Correctness of the algorithm

The logic behind this algorithm may not seem obvious at a first sight, however if we put together all the equations we have written so far, things will be clearer.

Let’s start from $P = u_1 G + u_2 H_A$. We know, from the definition of public key, that $H_A = d_A G$ (where $d_A$ is the private key). We can write: $$\begin{align*} P & = u_1 G + u_2 H_A \\ & = u_1 G + u_2 d_A G \\ & = (u_1 + u_2 d_A) G \end{align*}$$

Using the definitions of $u_1$ and $u_2$, we can write: $$\begin{align*} P & = (u_1 + u_2 d_A) G \\ & = (s^{-1} z + s^{-1} r d_A) G \\ & = s^{-1} (z + r d_A) G \end{align*}$$

Here we have omitted “$\text{mod}\ n$” both for brevity, and because the cyclic subgroup generated by $G$ has order $n$, hence “$\text{mod}\ n$” is superfluous.

Previously, we defined $s = k^{-1} (z + rd_A) \bmod{n}$. Multiplying each side of the equation by $k$ and dividing by $s$, we get: $k = s^{-1} (z + rd_A) \bmod{n}$. Substituting this result in our equation for $P$, we get: $$\begin{align*} P & = s^{-1} (z + r d_A) G \\ & = k G \end{align*}$$

This is the same equation for $P$ we had at step 2 of the signature generation algorithm! When generating signatures and when verifying them, we are calculating the same point $P$, just with a different set of equations. This is why the algorithm works.

Playing with ECDSA

Of course, I’ve created a Python script for signature generation and verification. The code shares some parts with the ECDH script, in particular the domain parameters and the public/private key pair generation algorithm.

Here is the kind of output produced by the script:

Curve: secp256k1
Private key: 0x9f4c9eb899bd86e0e83ecca659602a15b2edb648e2ae4ee4a256b17bb29a1a1e
Public key: (0xabd9791437093d377ca25ea974ddc099eafa3d97c7250d2ea32af6a1556f92a, 0x3fe60f6150b6d87ae8d64b78199b13f26977407c801f233288c97ddc4acca326)

Message: b'Hello!'
Signature: (0xddcb8b5abfe46902f2ac54ab9cd5cf205e359c03fdf66ead1130826f79d45478, 0x551a5b2cd8465db43254df998ba577cb28e1ee73c5530430395e4fba96610151)
Verification: signature matches

Message: b'Hi there!'
Verification: invalid signature

Message: b'Hello!'
Public key: (0xc40572bb38dec72b82b3efb1efc8552588b8774149a32e546fb703021cf3b78a, 0x8c6e5c5a9c1ea4cad778072fe955ed1c6a2a92f516f02cab57e0ba7d0765f8bb)
Verification: invalid signature

As you can see, the script first signs a message (the byte string “Hello!”), then verifies the signature. Afterwards, it tries to verify the same signature against another message (“Hi there!”) and verification fails. Lastly, it tries to verify the signature against the correct message, but using another random public key and verification fails again.

The importance of k

When generating ECDSA signatures, it is important to keep the secret $k$ really secret. If we used the same $k$ for all signatures, or if our random number generator were somewhat predictable, an attacker would be able to find out the private key!

This is the kind of mistake made by Sony a few years ago. Basically, the PlayStation 3 game console can run only games signed by Sony with ECDSA. This way, if I wanted to create a new game for PlayStation 3, I couldn’t distribute it to the public without a signature from Sony. The problem is: all the signatures made by Sony were generated using a static $k$.

(Apparently, Sony’s random number generator was inspired by either XKCD or Dilbert.)

In this situation, we could easily recover Sony’s private key $d_S$ by buying just two signed games, extracting their hashes ($z_1$ and $z_2$) and their signatures ($(r_1, s_1)$ and $(r_2, s_2)$), together with the domain parameters. Here’s how:

• First off, note that $r_1 = r_2$ (because $r = x_P \bmod{n}$ and $P = kG$ is the same for both signatures).
• Consider that $(s_1 - s_2) \bmod{n} = k^{-1} (z_1 - z_2) \bmod{n}$ (this result comes directly from the equation for $s$).
• Now multiply each side of the equation by $k$: $k (s_1 - s_2) \bmod{n} = (z_1 - z_2) \bmod{n}$.
• Divide by $(s_1 - s_2)$ to get $k = (z_1 - z_2)(s_1 - s_2)^{-1} \bmod{n}$.

The last equation lets us calculate $k$ using only two hashes and their corresponding signatures. Now we can extract the private key using the equation for $s$: $$s = k^{-1}(z + rd_S) \bmod{n}\ \ \Rightarrow\ \ d_S = r^{-1} (sk - z) \bmod{n}$$

Similar techniques may be employed if $k$ is not static but predictable in some way.

Have a great weekend

I really hope you enjoyed what I’ve written here. As usual, don’t hesitate to leave a comment or send me a poke if you need help with something.

Next week I’ll publish the fourth and last article of this series. It’ll be about techniques for solving discrete logarithms, some important problems of Elliptic Curve cryptography, and how ECC compares with RSA. Don’t miss it!

Read the next post of the series »